Arpeggiate by numbers
Workaday automatic composition and sequencing
January 8, 2015 — September 20, 2021
Where my audio software frameworks page does more DSP, this is mostly about MIDI—choosing notes, not timbres. A cousin of generative art with machine learning, with less AI and more UX.
Sometime you don’t want to measure a chord, or hear a chord, you just want to write a chord.
See also machine listening, musical corpora, musical metrics, synchronisation. The discrete, symbolic cousin to analysis/resynthesis.
Related projects: How I would do generative art with neural networks and learning gamelan.
1 Sonification
MIDITime maps time series data onto notes with some basic music theory baked in.
2 Geometric approaches
Dmitri Tymozcko claims, music data is most naturally regarded as existing on an orbifold (“quotient manifold”), which I’m sure you could do some clever regression upon, but I can’t yet see how. Orbifolds are, AFAICT, something like what you get when you have a bag of regressors instead of a tuple, and evoke the string bag models of the natural language information retrieval people, except there is not as much hustle for music as there is for NLP. Nonetheless manifold regression is a thing, and regression on manifolds is also a thing, so there is surely some stuff to be done there. Various complications arise; For example: it’s not a single scalar (which note) we are predicting at each time step, but some kind of joint distribution over several notes and their articulations. Or it is even sane to do this one step at a time? Lengthy melodic figures and motifs dominate in real compositions; how do you represent those tractably?
Further, it’s the joint distribution of the evolution of the harmonics and the noise and all that other timbral content that our ear can resolve, not just the symbolic melody. And we know from psycho-acoustics that these will be coupled— dissonance of two tones depends on frequency and amplitude of the spectral components of each, to name one commonly-postulated factor.
In any case, these wrinkles aside, if I could predict the conditional distribution of the sequence in a way that produced recognisably musical sound, then simulate from it, I would be happy for a variety of reasons. So I guess if I cracked this problem in the apparently direct way it might be by “nonparametric vector regression on an orbifold”, but with possibly heroic computation-wrangling en route.
3 Neural approaches
Musenet is a famous current one from OpenAI
We’ve created MuseNet, a deep neural network that can generate 4-minute musical compositions with 10 different instruments, and can combine styles from country to Mozart to the Beatles. MuseNet was not explicitly programmed with our understanding of music, but instead discovered patterns of harmony, rhythm, and style by learning to predict the next token in hundreds of thousands of MIDI files. MuseNet uses the same general-purpose unsupervised technology as GPT-2, a large-scale transformer model trained to predict the next token in a sequence, whether audio or text.
Google’s Magenta produces some sorta-interesting stuff, or at least stuff I always feel sis so close to actually being interesting without quite making it. Midi-me a light trsnfer learning(?) approach to personalising an overfit or overlarge midi composition model looks like a potentially nice hack, for example.
4 Composition assistants
4.1 Nestup
Totally my jam! A context-free tempo grammar for musical beats. Free.
Nestup. cutelabnyc/nested-tuplets: Fancy javascript for manipulating nested tuplets.
4.2 Scaler
Scaler 2 can listen to incoming MIDI or audio data and detect the key your music is in. It will suggest chords and chord progressions that will fit with your song. Scaler 2 can send MIDI to a virtual instrument in your DAW, but it also has 30 onboard instruments to play with as well.
4.3 J74
⭐⭐⭐⭐ (EUR12 + EUR15)
J74 progressive and J74 bassline by Fabrizio Poce’s apps are chord progression generators built with Ableton Live’s scripting engine, so if you are using Ableton they might be handy. I was using them myself, although I quit Ableton for bitwig, and although I enjoyed them I also don’t miss them. They did make Ableton crash on occasion, so not suited for live performance, which is a pity because that would be a wonderful value proposition if it were. The real-time-oriented J74 HarmoTools from the same guy are less sophisticated but worth trying, especially since they are free, and he has lot of other clever hacks there too. Do go to this guy’s site and try his stuff out.
4.4 Helio
⭐⭐⭐⭐ Free
Helio is free and cross platform and totally worth a shot. There is a chord model in there and version control (!) but you might not notice the chord thing if you aren’t careful, because the UI is idiosyncratic. Great for left-field inspiration, if not a universal composition tool.
4.5 Orca
Free, open source. ⭐⭐⭐⭐
Orca is a bespoke, opinionated weird grid-based programmable sequencer. It doesn’t aspire to solve every composition problem, but it does guarantee weird, individual, quirky algorithmic mayhem. It’s made by two people who live on a boat.
It can run in a browser.
4.6 Hookpad
⭐⭐⭐ (Freemium/USD149)
Hookpad is a spin-off of cult pop analysis website Hook Theory. I ran into it later than Odesi, so I frame my review in terms of Odesi, but it might be older. Compared to Odesi it has the same weakness by being a webapp. However, by being basically, just a webpage instead of a multi-gigabyte monster app with the restrictions of a web page, it is less aggravating than Odesi. It assumes a little (but not much) more music theory from the user. Also a plus, it is attached to an excellent library of pop song chord procession examples and analysis in the form of the (recommended) Hook Theory site.
4.7 Odesi
⭐⭐ (USD49)
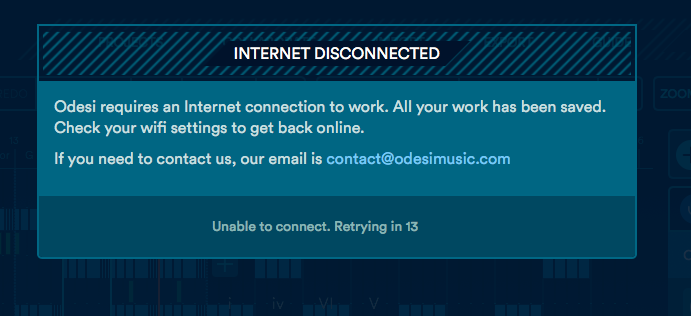
Odesi has been doing lots of advertising of their poptastic interface to generate pop music. It’s like Synfire-lite, with a library of top-40 melody tricks and rhythms. The desktop version tries to install gigabytes of synths of meagre merit on your machine, which is a giant waste of space and time if you are using a computer which already has synths on, which you are because this is not the 90s, and in any case you presumably have this app because you are already a music producer and therefore already have synths. However, unlike 90s apps, it requires you to be online, which is dissatisfying if you like to be offline in your studio so you can get shit done without distractions. So aggressive is it in its desire to be online, that any momentary interruption in your internet connection causes the interface to hang for 30 seconds, presenting you with a reassurance that none of your work is lost. Then it reloads, with some of your work nonetheless lost. A good idea marred by an irritating execution that somehow combines the worst of webapps and desktop apps.
4.8 Intermorphic
USD25/USD40
Intermorphic’s Mixtikl and Noatikl are granddaddy esoteric composer apps, although the creators doubtless put much effort into their groundbreaking user interfaces, I nonetheless have not used them because of the marketing material, which is notable for a inability to explain their app or provide compelling demonstrations or use cases. I get the feeling they had high-art aspirations but have ended up doing ambient noodles in order to sell product. Maybe I’m not being fair. If I find spare cash at some point I will find out.
4.9 Rozeta
Ruismaker’s Rozeta (iOS) has a series of apps producing every nifty fashionable sequencer algorithm in recent memory. I don’t have an ipad though, so I will not review them.
4.10 Rapid compose
Rapid Compose (USD99/USD249) might make decent software, but can’t clearly explain why their app is nice or provide a demo version.
4.11 Synfire
EUR996, so I won’t be buying it, but wow, what a demo video.
synfire explains how it uses music theory to do large-scale scoring etc. Get the string section to behave itself or you’ll replace them with MIDIbots.
4.12 Harmony Builder
USD39-USD219 depending on heinously complex pricing schemes.
Harmony builder does classical music theory for you. Will pass your conservatorium finals.
4.13 Roll your own
You can’t resist rolling your own?
sharp11 is a node.js music theory library for javascript with demo application to create jazz improv.
Supercollider of course does this like it does everything else, which is to say, quirkily-badly. Designing user interfaces for it takes years off your life. OTOH, if you are happy with text, this might be a goer.
5 Arpeggiators
- Bluearp vst does 2-note chord extrapolation (free)
- Hypercyclic is an LFO-able arpeggiator (free)
- kirnu cream (EUR35) is a friendly VST for fancy chord wiggling
- Polyrhythmus (Max 4 live only)
6 Constraint Composition
All of that too mainstream? Try a weird alternative formalism! How about constraint composition? That is, declarative musical composition by defining constraints on the relations which the notes must satisfy. Sounds fun in the abstract but the practice doesn’t grab me especially as a creative tool.
The reference tool for that purpose seem to be strasheela built on an obscure, unpopular, and apparently discontinued Prolog-like language called “Oz” or “Mozart”, because using popular languages is not a grand a gesture as claiming none of them are quite Turing-complete enough, in the right way, for your special snowflake application. That language is a ghost town, which means headaches if you wish to use Strasheela practice; If you wanted to actually use constraint methods, you’d probably use overtone + minikanren (prolog-for-lisp), as with the composing schemer, or to be even more mainstream, just use a conventional constraint solver in a popular language. I am fond of python and ncvx, but there are many choices.
Anyway, prolog fans can read on: see Anders and Miranda (2010);Anders and Miranda (2011).
7 Random ideas
- How would you reconstruct a piece from its recurrence matrix? or at least constrain pieces by their recurrence matrix?
8 Incoming
- Music Transformer: Generating Music with Long-Term Structure
- MuseNet
- ReBoard - an interval basel Midi Player - Soundmanufacture “ReBoard - is a Max for Live Device based on the very simple Idea to play relative notes within a given scale. The name ReBoard is derived from Re_lative Key_board.”