Knowledge geometry

1 What is the shape of collected human knowledge?

This is vague.

I do not know how to make this idea precise yet, but I would like to spitball a few ideas about how branches of knowledge might be adjacent to each other or not, in various senses.

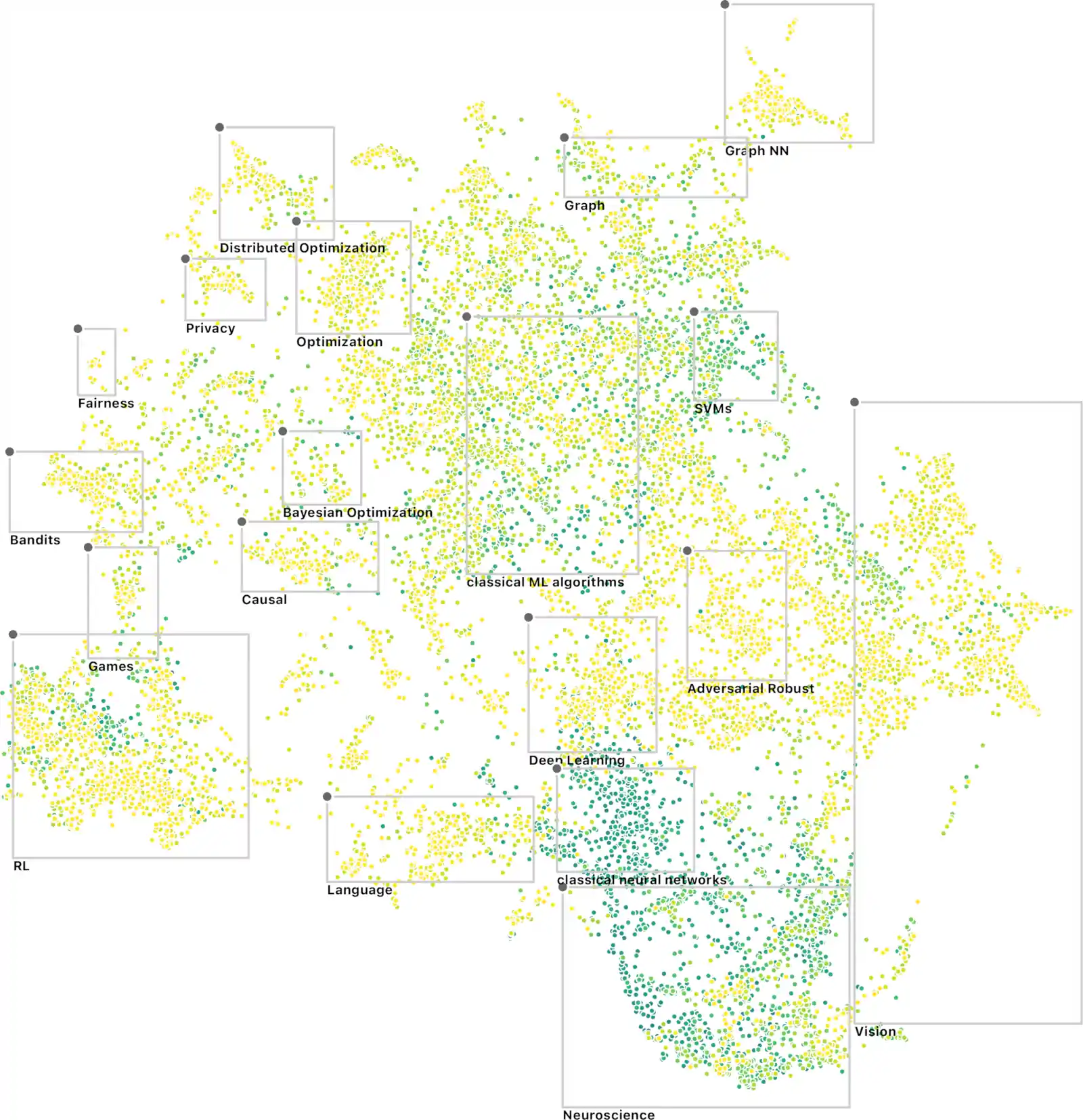
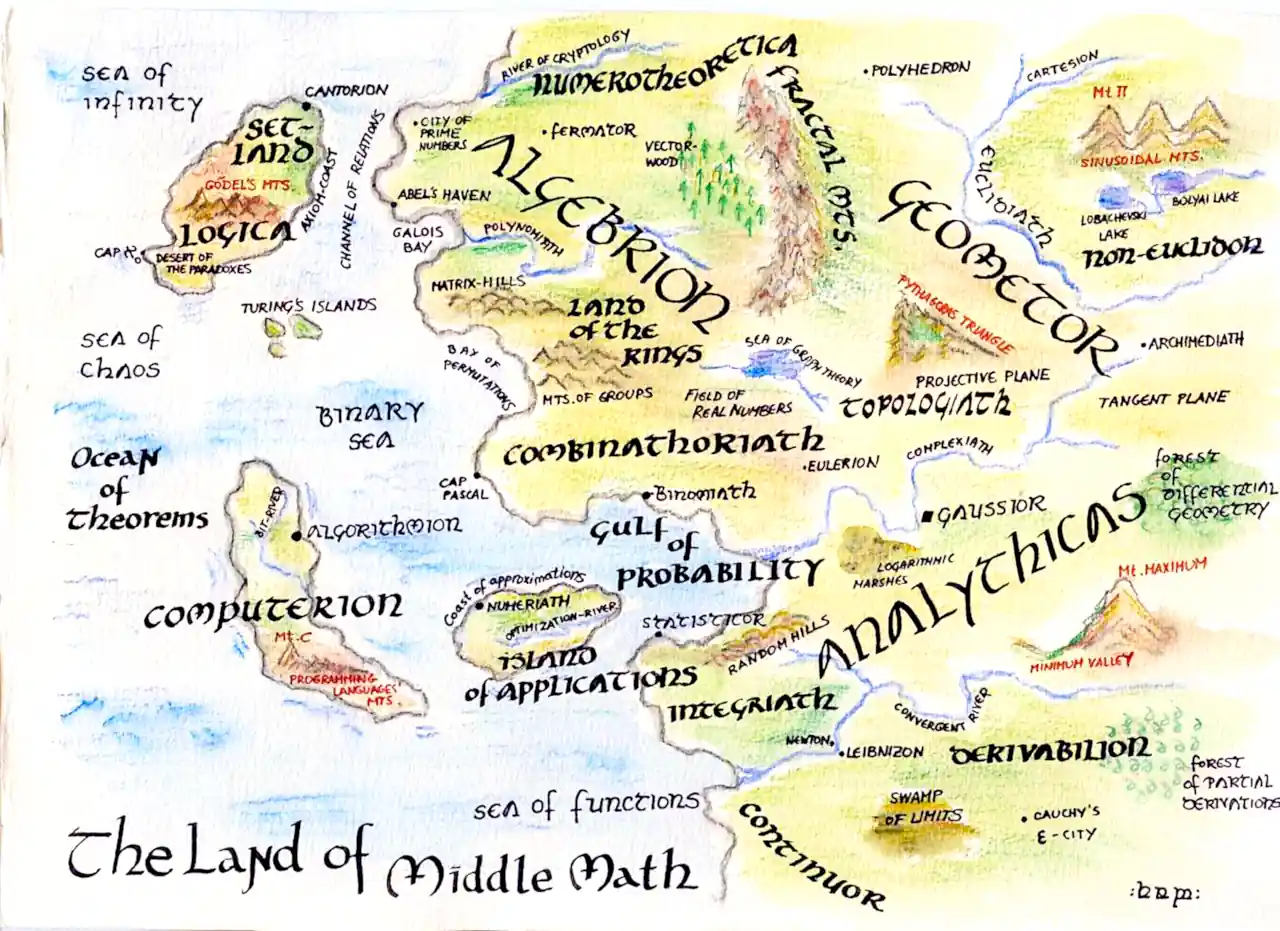
For example, what metric space provides a natural embedding for the articles of an encyclopedia such that things that articles that are near in (the metric of) that space possess similar subject classifications? I have seen arguments that hyperbolic and other non-euclidean geometries arise here. But then, because our monkey minds work this way, we seem to project knowledge onto 2d euclidean maps, and it seems to be at least interesting:

What kind of knowledge relationship mechanisms are plausible? Could you mine patent networks or theorem networks to parameterise a stochastic process for this model which made it a plausible model for theorem growth? If not, what quality does knowledge posses which this could not encapsulate? If we have a good metric on knowledge that we can learn from (e.g.) the text of papers, can we use it to discover similar research? Or to identify lacunae in knowledge that we can fill?

Or should we think about the mechanism of knowledge generation? Can we represent knowledge as a network (or a landscape?) that accretes around agent activity? Some kind of growth process around researchers? (keywords: “models of growth aggregation”, “rough interfaces”, “growth with surface diffusion”, “nucleation”, “morphogenesis”) Is this a constrained growth problem, like the one that governs coral drills?

Investigate configuration spaces of technologies. (See configuration space of the economy.) Genotype-phenotype interactions as a model of knowledge-economic systems? What is the most basic stochastic process that would serve as a model of these?

(Practical aside: How much area must a new thesis carve out from the unmade world?)

Now, going out on a limb, consider a problem domain that looks evolutionary if you squint at it: creating mathematical theorems. Certainly Gödel and Turing invite looking at the things as symbol strings. I saw a presentation (Leibon and Rockmore 2013) suggesting that there was a natural embedding of mathematical field onto hyperbolic geometry. Sure, his data set was Wikipedia mathematical article links, and the whole idea was tongue-in-cheek. But it feels like there is something in there, if not a whole-cloth topological theory of human knowledge. Is there some process driving mathematical innovation that means that the links between fields sit so naturally in hyperbolic space? Is it some characteristic of the subject matter itself? If either of these are true, would they be true of other fields? Science in general? Philosophy? Engineering? Design? Biological fitnesses?

2 To Investigate, possibly related

3 Related links

Many, many try to construct a network topology for citation networks There are enough that the citation network citation network is already a non trivial dataset to study. If you publish on that dataset in particular you bring us clsoer to the day when we can discuss the citation network citation network citation network.

Here’s one step down that road:

• KWRegan’s Connect the Stars: How papers are like constellations

• Microsoft Academic Knowledge Graph

  We present the Microsoft Academic Knowledge Graph (MAKG), a large RDF data set with over eight billion triples with information about scientific publications and related entities, such as authors, institutions, journals, and fields of study. The data set is based on the Microsoft Academic Graph and licensed under the Open Data Attributions license. Furthermore, we provide entity embeddings for all 210M represented scientific papers.

4 References