Learning of manifolds
Also topological data analysis; other hip names to follow
August 19, 2014 — June 23, 2020
🏗🏗🏗🏗🏗
I will restructure learning on manifolds and dimensionality reduction into a more useful distinction.
As in — handling your high-dimensional, or graphical, data by trying to discover a low(er)-dimensional manifold that contains it. That is, inferring a hidden constraint that happens to have the form of a smooth surface of some low-ish dimension. related: Learning on manifolds, and if you squint at it, learnable indexes.
There are a million different versions of this. Multidimensional scaling seems to be the oldest.
Tangential aside: in dynamical systems we talk about creating high dimensional Takens embedding for state space reconstruction for arbitrary nonlinear dynamics. I imagine there are some connections between learning the lower-dimensional manifold upon which lies your data, and the higher dimensional manifold in which your data’s state space is naturally expressed. But I would not be the first person to notice this, so hopefully it’s done for me somewhere?
See also kernel methods, and functional regression, which connects via diffusion maps (Ronald R. Coifman and Lafon 2006; R. R. Coifman et al. 2005, 2005).
See also information geometry, which uses manifolds also but one implied by the parameterisation of a parametric model.
To look at: ISOMAP, Locally linear embedding, spectral embeddings, diffusion maps, multidimensional scaling…
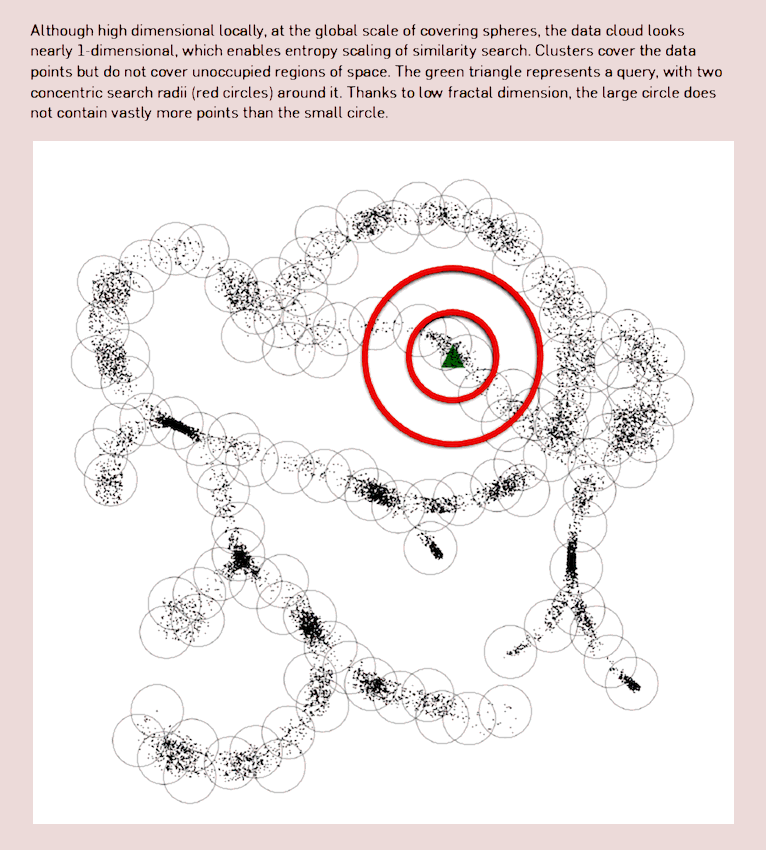
Bioinformatics is leading to some weird use of data manifolds; see for example Berger, Daniels, and Yu (2016) for the performance implications of knowing the manifold shape for *-omics search, using compressive manifold storage based on both fractal dimension and metric entropy concepts. Also suggestive connection with fitness landscape in evolution.
Neural networks have some implicit manifolds, if you squint right. see Christopher Olahs’s visual explanation how, whose diagrams should be stolen by someone trying to explain V-C dimension.
Berger, Daniels, and Yu (2016) argue:
Manifold learning algorithms have recently played a crucial role in unsupervised learning tasks such as clustering and nonlinear dimensionality reduction […] Many such algorithms have been shown to be equivalent to Kernel PCA (KPCA) with data dependent kernels, itself equivalent to performing classical multidimensional scaling (cMDS) in a high dimensional feature space (Schölkopf et al., 1998; Williams, 2002; Bengio et al., 2004). […] Recently, it has been observed that the majority of manifold learning algorithms can be expressed as a regularized loss minimization of a reconstruction matrix, followed by a singular value truncation (Neufeld et al., 2012)
1 Implementations
1.1 TTK
The Topology ToolKit (TTK) is an open-source library and software collection for topological data analysis in scientific visualization.
TTK can handle scalar data defined either on regular grids or triangulations, either in 2D or in 3D. It provides a substantial collection of generic, efficient and robust implementations of key algorithms in topological data analysis. It includes:
For scalar data: critical points, integral lines, persistence diagrams, persistence curves, merge trees, contour trees, Morse-Smale complexes, topological simplification;
For bivariate scalar data: fibers, fiber surfaces, continuous scatterplots, Jacobi sets, Reeb spaces;
For uncertain scalar data: mandatory critical points;
1.2 scikit-learn
scikit-learn implements a grab-bag of algorithms
1.3 tapkee
C++: Tapkee. Pro-tip — even without coding, tapkee does a long list of nice dimensionality reduction from the CLI, some of which are explicitly manifold learners (and the rest are matrix factorisations which is not so different)
- Locally Linear Embedding and Kernel Locally Linear Embedding (LLE/KLLE)
- Neighborhood Preserving Embedding (NPE)
- Local Tangent Space Alignment (LTSA)
- Linear Local Tangent Space Alignment (LLTSA)
- Hessian Locally Linear Embedding (HLLE)
- Laplacian eigenmaps
- Locality Preserving Projections
- Diffusion map
- Isomap and landmark Isomap
- Multidimensional scaling and landmark Multidimensional scaling (MDS/lMDS)
- Stochastic Proximity Embedding (SPE)
- PCA and randomized PCA
- Kernel PCA (kPCA)
- t-SNE
- Barnes-Hut-SNE