Approximate matrix factorisations and decompositions

Sometimes even exact

August 5, 2014 — August 23, 2023

feature construction
functional analysis
high d
linear algebra
networks
probability
signal processing
sparser than thou
statistics

Assumed audience:

People with undergrad linear algebra

Figure 1

1 The classics

The big six exact matrix decompositions are (Stewart 2000)

  • Cholesky decomposition
  • pivoted LU decomposition
  • QR decomposition
  • spectral decomposition
  • Schur decomposition; and
  • singular value decomposition.

See Nick Higham’s summary of those.

2 Approximate decompositions

Mastered QR and LU decompositions? There are now so many ways of factorising matrices that there are not enough acronyms in the alphabet to hold them, especially if we suspect our matrix is sparse, or could be made sparse because of some underlying constraint, or probably could, if squinted at in the right fashion, be such as a graph transition matrix, or Laplacian, or noisy transform of some smooth object, or at least would be close to sparse if we chose the right metric, or…

A big matrix is close to, in some sense, the (tensor/matrix) product (or sum, or…) of some matrices that are in some way simple (small-rank, small dimension, sparse), possibly with additional constraints. Can we find those simple matrices?

Ethan Epperly’s introduction to Low-rank Matrices puts many ideas clearly.

Here’s an example: Godec (T. Zhou and Tao 2011) — A decomposition into low-rank and sparse components which loosely speaking, combines multidimensional factorisation and outlier detection.

GoDec is one of the most efficient algorithm for low-rank and sparse decomposition thanks to bilateral random projections (BRP), a fast approximation of SVD/PCA.

There are so many more of these things, depending on our preferred choice of metric, constraints, free variables and such.

Keywords: Matrix sketching, low-rank approximation, traditional dimensionality reduction.

Matrix concentration inequalities turn out to a useful tool to prove that a given matrix decomp is not too bad in a PAC-sense.

Igor Carron’s Matrix Factorization Jungle classifies the following problems as matrix-factorisation type.

Kernel Factorizations
…
Spectral clustering
\([\mathrm{A} = \mathrm{D} \mathrm{X}]\) with unknown \(\mathrm{D}\) and \(\mathrm{X}\), solve for sparse \(\mathrm{X}\) and \(\mathrm{X}_i = 0\) or \(1\)
K-Means / K-Median clustering
\([\mathrm{A} = \mathrm{D} \mathrm{X}]\) with unknown and , solve for \(\mathrm{X} \mathrm{X}^{\top} = \mathrm{I}\) and \(\mathrm{X}_i = 0 or 1\)
Subspace clustering
\([\mathrm{A} = \mathrm{A} \mathrm{X}]\) with unknown \(\mathrm{X}\), solve for sparse/other conditions on \(\mathrm{X}\)
Graph Matching
\([\mathrm{A} = \mathrm{X} \mathrm{B} \mathrm{X} ^{\top}]\) with unknown \(\mathrm{X}\), \(\mathrm{B}\) solve for \(\mathrm{B}\) and \(\mathrm{X}\) as a permutation
NMF
\([\mathrm{A} = \mathrm{D} \mathrm{X}]\) with unknown \(\mathrm{D}\) and \(\mathrm{X}\), solve for elements of \(\mathrm{D}\),\(\mathrm{X}\) positive
Generalized Matrix Factorization
\([\mathrm{W}.*\mathrm{L} − \mathrm{W}.*\mathrm{U} \mathrm{V}']\) with \(\mathrm{W}\) a known mask, \(\mathrm{U}\),\(\mathrm{V}\) unknowns solve for \(\mathrm{U}\),\(\mathrm{V}\) and \(\mathrm{L}\) lowest rank possible
Matrix Completion
\([\mathrm{A} = \mathrm{H}.*\mathrm{L}]\) with \(\mathrm{H}\) a known mask, \(\mathrm{L}\) unknown solve for \(\mathrm{L}\) lowest rank possible
Stable Principle Component Pursuit (SPCP)/ Noisy Robust PCA
\([\mathrm{A} = \mathrm{L} + \mathrm{S} + \mathrm{N}]\) with \(\mathrm{L}\), \(\mathrm{S}\), \(\mathrm{N}\) unknown, solve for \(\mathrm{L}\) low rank, \(\mathrm{S}\) sparse, \(\mathrm{N}\) noise
Robust PCA
\([\mathrm{A} = \mathrm{L} + \mathrm{S}]\) with , unknown, solve for \(\mathrm{L}\) low rank, \(\mathrm{S}\) sparse
Sparse PCA
\([\mathrm{A} = \mathrm{D} \mathrm{X} ]\) with unknown \(\mathrm{D}\) and \(\mathrm{X}\), solve for sparse \(\mathrm{D}\)
Dictionary Learning
\([\mathrm{A} = \mathrm{D} \mathrm{X}]\) with unknown \(\mathrm{D}\) and \(\mathrm{X}\), solve for sparse \(\mathrm{X}\)
Archetypal Analysis
\([\mathrm{A} = \mathrm{D} \mathrm{X}]\) with unknown \(\mathrm{D}\) and \(\mathrm{X}\), solve for \(\mathrm{D}= \mathrm{A} \mathrm{B}\) with \(\mathrm{D}\), \(\mathrm{B}\) positive
Matrix Compressive Sensing (MCS)
find a rank-r matrix \(\mathrm{L}\) such that \([\mathrm{A}(\mathrm{L}) ~= b]\) / or \([\mathrm{A}(\mathrm{L}+\mathrm{S}) = b]\)
Multiple Measurement Vector (MMV)
\([\mathrm{Y} = \mathrm{A} \mathrm{X}]\) with unknown \(\mathrm{X}\) and rows of \(\mathrm{X}\) are sparse
Compressed sensing
\([\mathrm{Y} = \mathrm{A} \mathrm{X}]\) with unknown \(\mathrm{X}\) and rows of \(\mathrm{X}\) are sparse, \(\mathrm{X}\) is one column.
Blind Source Separation (BSS)
\([\mathrm{Y} = \mathrm{A} \mathrm{X}]\) with unknown \(\mathrm{A}\) and \(\mathrm{X}\) and statistical independence between columns of \(\mathrm{X}\) or subspaces of columns of \(\mathrm{X}\)
Partial and Online SVD/PCA
…
Tensor Decomposition
Many, many options; see tensor decompositions for some tractable ones.

Truncated Classic PCA is clearly also an example, but is excluded from the list for some reason. Boringness? the fact it’s a special case of Sparse PCA?

I also add

Square root
\(\mathrm{Y} = \mathrm{X}^{\top}\mathrm{X}\) for \(\mathrm{Y}\in\mathbb{R}^{N\times N}, X\in\mathbb{R}^{N\times n}\), with (typically) \(n<N\).

That is a whole thing; see matrix square root.

See also learning on manifolds, compressed sensing, optimisation random linear algebra and clustering, penalised regression…

3 Tutorials

4 Non-negative matrix factorisations

See non-negative matrix factorisations.

5 Why is approximate factorisation ever useful?

For certain types of data matrix, here is a suggestive observation: Udell and Townsend (2019) ask “Why Are Big Data Matrices Approximately Low Rank?”

Matrices of (approximate) low rank are pervasive in data science, appearing in movie preferences, text documents, survey data, medical records, and genomics. While there is a vast literature on how to exploit low rank structure in these datasets, there is less attention paid to explaining why the low rank structure appears in the first place. Here, we explain the effectiveness of low rank models in data science by considering a simple generative model for these matrices: we suppose that each row or column is associated to a (possibly high dimensional) bounded latent variable, and entries of the matrix are generated by applying a piecewise analytic function to these latent variables. These matrices are in general full rank. However, we show that we can approximate every entry of an \(m\times n\) matrix drawn from this model to within a fixed absolute error by a low rank matrix whose rank grows as \(\mathcal{O}(\log(m+n))\). Hence any sufficiently large matrix from such a latent variable model can be approximated, up to a small entrywise error, by a low rank matrix.

Ethan Epperly argues from a function approximation perspective (e.g.) that we can deduce this property from smoothness of functons.

Saul (2023) connects non-negative matrix factorisation to geometric algebra and linear algebra via deep learning and kernels. That sounds like fun.

6 As regression

Total Least Squares (a.k.a. orthogonal distance regression, or error-in-variables least-squares linear regression) is a low-rank matrix approximation that minimises the Frobenius divergence from the data matrix. Who knew?

Various other dimensionality reduction techniques can be put in a regression framing, notable Exponential-family PCA.

7 Sketching

“Sketching” is a common term to describe a certain type of low-rank factorisation, although I am not sure which types. 🏗

(Martinsson 2016) mentions CUR and interpolative decompositions. What is that now?

8 Randomization

Rather than find an optimal solution, why not just choose a random one which might be good enough? There are indeed randomised versions, and many algorithms are implemented using randomness and in particular low-dimensional projections.

9 Connections to kernel learning

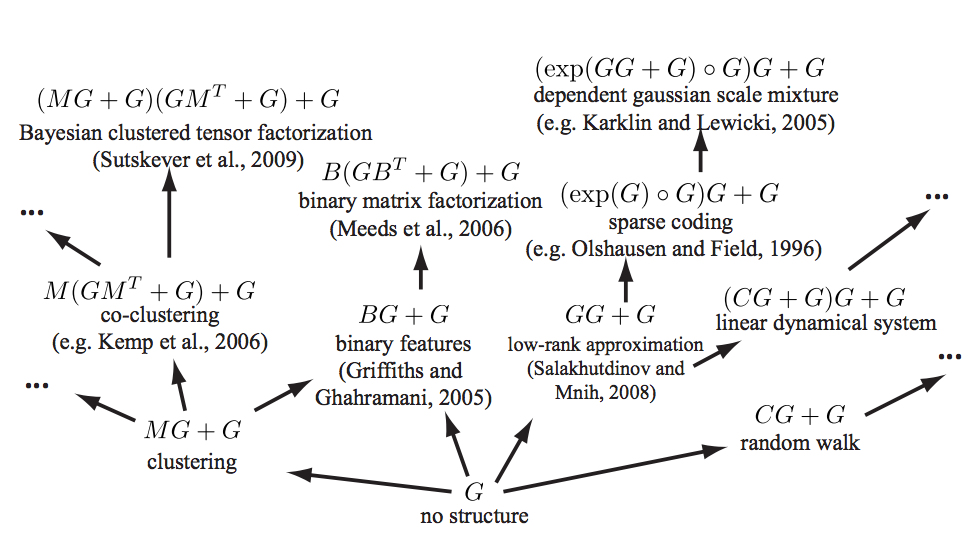
See (Grosse et al. 2012) for a mind-melting compositional matrix factorization diagram, constructing a search over hierarchical kernel decompositions that also turn out to have some matrix factorisation interpretations.

Figure 2: Exploiting compositionality to explore a large space of model structures

10 Bayesian

Nakajima and Sugiyama (2012):

Mnih and Salakhutdinov (2008) proposed a Bayesian maximum a posteriori (MAP) method based on the Gaussian noise model and Gaussian priors on the decomposed matrices. This method actually corresponds to minimizing the squared-loss with the trace-norm penalty (Srebro, Rennie, and Jaakkola 2004) Recently, the variational Bayesian (VB) approach (Attias 1999) has been applied to MF (Lim and Teh 2007; Raiko, Ilin, and Karhunen 2007), which we refer to as VBMF. The VBMF method was shown to perform very well in experiments. However, its good performance was not completely understood beyond its experimental success.

☜ Insert further developments here. Possibly Brouwer’s thesis (Brouwer 2017) or Shakir Mohamed’s (Mohamed 2011) would be a good start, or Benjamin Drave’s tutorial, Probabilistic Matrix Factorization and Xinghao Ding, Lihan He, and Carin (2011).

I am currently sitting in a seminar by He Zhao on Bayesian matrix factorisation, wherein he is building up this tool for discrete data, which is an interesting case. He starts from M. Zhou et al. (2012) and builds up to Zhao et al. (2018), introducing some hierarchical descriptions along the way. His methods seem to be sampling-based rather than variational (?).

Generalized² Linear² models (Gordon 2002) unify nonlinear matrix factorisations with Generalized Linear Models. I had not heard of that until recently; I wonder how common it is?

11 Lanczos decomposition

Lanczos decomposition is handy approximation for matrices which are cheap to multiply because of some structure, but expensive to store. It can also be used to calculate an approximate inverse cheaply.

I learnt this trick from Gaussian process literature in the context of Lanczos Variance Estimates (LOVE) (Pleiss et al. 2018), although I believe it exists elsewhere.

Given some rank \(k\) and an arbitrary starting vector \(\boldsymbol{b}\), the Lanczos algorithm iteratively approximates \(\mathrm{K} \in\mathbb{R}^{n \times n}\) by a low rank factorisation \(\mathrm{K}\approx \mathrm{Q} \mathrm{T} \mathrm{Q}^{\top}\), where \(\mathrm{T} \in \mathbb{R}^{k \times k}\) is tridiagonal and \(\mathrm{Q} \in \mathbb{R}^{n \times k}\) has orthogonal columns. Crucially, we do not need to form \(\mathrm{K}\) to evaluate matrix vector products \(\mathrm{K}\boldsymbol{b}\) for arbitrary vector \(\boldsymbol{b}\). Moreover, with a given Lanczos approximand \(\mathrm{Q},\mathrm{T}\) we may estimate \[\begin{align*} \mathrm{K}^{-1}\boldsymbol{c}\approx \mathrm{Q}\mathrm{T}^{-1}\mathrm{Q}^{\top}\boldsymbol{c}. \end{align*}\] even for \(\boldsymbol{b}\neq\boldsymbol{c}\). Say we wish to calculate \(\left(\mathrm{Z} \mathrm{Z}^{\top}+\sigma^2 \mathrm{I}\right)^{-1}\mathrm{B}\), with \(\mathrm{Z}\in\mathbb{R}^{D\times N }\) and \(N\ll D\).

We approximate the solution to this linear system using the partial Lanczos decomposition starting with probe vector \(\boldsymbol{b}=\overline{\mathrm{B}}\) and \(\mathrm{K}=\left(\mathrm{Z} \mathrm{Z}^{\top}+\sigma^2 \mathrm{I}\right)\).

This requires \(k\) matrix vector products of the form \[\begin{align*} \underbrace{\left(\underbrace{\mathrm{Z} \mathrm{Z}^{\top}}_{\mathcal{O}(ND^2)}+\sigma^2 \mathrm{I}\right)\boldsymbol{b}}_{\mathcal{O}(D^2)} =\underbrace{\mathrm{Z} \underbrace{(\mathrm{Z}^{\top}\boldsymbol{b})}_{\mathcal{O}(ND)}}_{\mathcal{O}(ND)} +\sigma^2 \boldsymbol{b}. \end{align*}\] Using the latter representation, the required matrix-vector product may be found with a time complexity cost of \(\mathcal{O}(ND)\). Space complexity is also \(\mathcal{O}(ND)\). The output of the Lanczos decomposition is \(\mathrm{Q},\mathrm{T}\) such that \(\left(\mathrm{Z}\mathrm{Z}^{\top} +\sigma^2 \mathrm{I}\right)\boldsymbol{b}\approx \mathrm{Q} \mathrm{T} \mathrm{Q}^{\top}\boldsymbol{b}\). Then the solution to the inverse-matrix-vector product may be approximated by \(\left(\mathrm{Z} \mathrm{Z}^{\top} +\sigma^2 \mathrm{I}\right)^{-1} \mathrm{B}\approx \mathrm{Q}\mathrm{T}^{-1}\mathrm{Q}^{\top}\mathrm{B}\). requiring the solution in \(\mathrm{X}\) of the much smaller linear system \(\mathrm{X}\mathrm{T}=\mathrm{Q}\). Exploiting the positive-definiteness of \(\mathrm{T}\) we may use the Cholesky decomposition of \(\mathrm{T}=\mathrm{L}^{\top}\mathrm{L}\) for a constant speedup over solving an arbitrary linear system. The time cost of the solution is \(\mathcal{O}(Dk^3)\), for an overall cost to the matrix inversions of \(\mathcal{O}(NDk+Dk^3)\).

12 Estimating rank

Overview — imate Manual

Eigencount and Numerical Rank

If \(f: \lambda \mapsto \mathbf{1}_{[a, b]}(\lambda)\) is the indicator (step) function in the interval \([a, b]\), then \(\operatorname{trace}(\mathbf{1}(\mathbf{A}))\) estimates the number of non-zero eigenvalues of \(\mathbf{A}\) in that interval, which is an inexpensive method to estimate the rank of a large matrix. Eigencount is closely related to the Principal Component Analysis (PCA) and lowrank approximations in machine learning.

13 Incremental decompositions

13.1 SVD

See incremental SVD.

13.2 Cholesky

14 Low rank plus diagonal

Specifically \((\mathrm{K}=\mathrm{Z} \mathrm{Z}^{\top}+\sigma^2\mathrm{I})\) where \(\mathrm{K}\in\mathbb{R}^{N\times N}\) and \(\mathrm{Z}\in\mathbb{R}^{N\times D}\) with \(D\ll N\). A workhorse.

Lots of fun tricks.

See low rank plus diagonal matrices.

15 Misc

16 As an optimisation problem

There are some generalised optimisation problems which look useful for matrix factorisation, e.g. Bhardwaj, Klep, and Magron (2021):

Polynomial optimization problems (POP) are prevalent in many areas of modern science and engineering. The goal of POP is to minimize a given polynomial over a set defined by finitely many polynomial inequalities, a semialgebraic set. This problem is well known to be NP-hard, and has motivated research for more practical methods to obtain approximate solutions with high accuracy.[…]

One can naturally extend the ideas of positivity and sums of squares to the noncommutative (nc) setting by replacing the commutative variables \(z_1, \dots , z_n\) with noncommuting letters \(x_1, \dots , x_n\). The extension to the noncommutative setting is an inevitable consequence of the many areas of science which regularly optimize functions with noncommuting variables, such as matrices or operators. For instance in control theory, matrix completion, quantum information theory, or quantum chemistry

Matrix calculus can help cometimes.

17 \([\mathcal{H}]\)-matrix methods

It seems like low-rank matrix factorisation could related to \([\mathcal{H}]\)-matrix methods, but I do not know enough to say more.

See hmatrix.org for one lab’s backgrounder and their implementation, h2lib, hlibpro for a black-box closed-source one.

18 Tools

In pytorch, various operations are made easier with cornellius-gp/linear_operator.

Ameli’s tools:

NMF Toolbox (MATLAB and Python):

Nonnegative matrix factorization (NMF) is a family of methods widely used for information retrieval across domains including text, images, and audio. Within music processing, NMF has been used for tasks such as transcription, source separation, and structure analysis. Prior work has shown that initialization and constrained update rules can drastically improve the chances of NMF converging to a musically meaningful solution. Along these lines we present the NMF toolbox, containing MATLAB and Python implementations of conceptually distinct NMF variants—in particular, this paper gives an overview for two algorithms. The first variant, called nonnegative matrix factor deconvolution (NMFD), extends the original NMF algorithm to the convolutive case, enforcing the temporal order of spectral templates. The second variant, called diagonal NMF, supports the development of sparse diagonal structures in the activation matrix. Our toolbox contains several demo applications and code examples to illustrate its potential and functionality. By providing MATLAB and Python code on a documentation website under a GNU-GPL license, as well as including illustrative examples, our aim is to foster research and education in the field of music processing.

Vowpal Wabbit factors matrices, e.g for recommender systems. It seems the --qr version is more favoured.

HPC for matlab, R, python, c++: libpmf:

LIBPMF implements the CCD++ algorithm, which aims to solve large-scale matrix factorization problems such as the low-rank factorization problems for recommender systems.

Spams (C++/MATLAB/python) includes some matrix factorisations in its sparse approx toolbox. (see optimisation)

scikit-learn (python) does a few matrix factorisation in its inimitable batteries-in-the-kitchen-sink way.

nimfa

… is a Python library for nonnegative matrix factorization. It includes implementations of several factorization methods, initialization approaches, and quality scoring. Both dense and sparse matrix representation are supported.”

Tapkee (C++). Pro-tip — even without coding C++, tapkee does a long list of dimensionality reduction from the CLI.

  • PCA and randomized PCA
  • Kernel PCA (kPCA)
  • Random projection
  • Factor analysis

tensorly supports some interesting tensor decompositions.

19 References

Aarabi, and Peeters. 2018. “Music Retiler: Using NMF2D Source Separation for Audio Mosaicing.” In Proceedings of the Audio Mostly 2018 on Sound in Immersion and Emotion. AM’18.
Abdallah, and Plumbley. 2004. “Polyphonic Music Transcription by Non-Negative Sparse Coding of Power Spectra.” In.
Achlioptas. 2003. “Database-Friendly Random Projections: Johnson-Lindenstrauss with Binary Coins.” Journal of Computer and System Sciences, Special Issue on PODS 2001,.
Aghasi, Nguyen, and Romberg. 2016. “Net-Trim: A Layer-Wise Convex Pruning of Deep Neural Networks.” arXiv:1611.05162 [Cs, Stat].
Akimoto. 2017. “Fast Eigen Decomposition for Low-Rank Matrix Approximation.”
Ameli, and Shadden. 2023. “A Singular Woodbury and Pseudo-Determinant Matrix Identities and Application to Gaussian Process Regression.” Applied Mathematics and Computation.
Ang, and Gillis. 2018. “Accelerating Nonnegative Matrix Factorization Algorithms Using Extrapolation.” Neural Computation.
Arora, Ge, Halpern, et al. 2012. “A Practical Algorithm for Topic Modeling with Provable Guarantees.” arXiv:1212.4777 [Cs, Stat].
Attias. 1999. “Inferring Parameters and Structure of Latent Variable Models by Variational Bayes.” In Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence. UAI’99.
Babacan, Luessi, Molina, et al. 2012. “Sparse Bayesian Methods for Low-Rank Matrix Estimation.” IEEE Transactions on Signal Processing.
Bach, Francis R. 2013. “Sharp Analysis of Low-Rank Kernel Matrix Approximations.” In COLT.
Bach, Francis. 2013. “Convex Relaxations of Structured Matrix Factorizations.” arXiv:1309.3117 [Cs, Math].
Bach, C, Ceglia, Song, et al. 2019. “Randomized Low-Rank Approximation Methods for Projection-Based Model Order Reduction of Large Nonlinear Dynamical Problems.” International Journal for Numerical Methods in Engineering.
Bach, Francis, Jenatton, and Mairal. 2011. Optimization With Sparsity-Inducing Penalties. Foundations and Trends(r) in Machine Learning 1.0.
Bach, Francis R, and Jordan. 2002. “Kernel Independent Component Analysis.” Journal of Machine Learning Research.
Bagge Carlson. 2018. “Machine Learning and System Identification for Estimation in Physical Systems.”
Barbier, Macris, and Miolane. 2017. “The Layered Structure of Tensor Estimation and Its Mutual Information.” arXiv:1709.10368 [Cond-Mat, Physics:math-Ph].
Bardenet, and Maillard. 2015. “A Note on Replacing Uniform Subsampling by Random Projections in MCMC for Linear Regression of Tall Datasets.”
Batson, Spielman, and Srivastava. 2008. “Twice-Ramanujan Sparsifiers.” arXiv:0808.0163 [Cs].
Bauckhage. 2015. “K-Means Clustering Is Matrix Factorization.” arXiv:1512.07548 [Stat].
Berry, Browne, Langville, et al. 2007. “Algorithms and Applications for Approximate Nonnegative Matrix Factorization.” Computational Statistics & Data Analysis.
Bertin, Badeau, and Vincent. 2010. “Enforcing Harmonicity and Smoothness in Bayesian Non-Negative Matrix Factorization Applied to Polyphonic Music Transcription.” IEEE Transactions on Audio, Speech, and Language Processing.
Bhardwaj, Klep, and Magron. 2021. “Noncommutative Polynomial Optimization.”
Brand. 2002. “Incremental Singular Value Decomposition of Uncertain Data with Missing Values.” In Computer Vision — ECCV 2002.
———. 2006. “Fast Low-Rank Modifications of the Thin Singular Value Decomposition.” Linear Algebra and Its Applications, Special Issue on Large Scale Linear and Nonlinear Eigenvalue Problems,.
Brouwer. 2017. “Bayesian Matrix Factorisation: Inference, Priors, and Data Integration.”
Bruckstein, Elad, and Zibulevsky. 2008a. “Sparse Non-Negative Solution of a Linear System of Equations Is Unique.” In 3rd International Symposium on Communications, Control and Signal Processing, 2008. ISCCSP 2008.
———. 2008b. “On the Uniqueness of Nonnegative Sparse Solutions to Underdetermined Systems of Equations.” IEEE Transactions on Information Theory.
Buch, Quinton, and Sturm. 2017. “NichtnegativeMatrixFaktorisierungnutzendesKlangsynthesenSystem (NiMFKS): Extensions of NMF-Based Concatenative Sound Synthesis.” In Proceedings of the 20th International Conference on Digital Audio Effects.
Bunch, and Nielsen. 1978. “Updating the Singular Value Decomposition.” Numerische Mathematik.
Caetano, and Rodet. 2013. “Musical Instrument Sound Morphing Guided by Perceptually Motivated Features.” IEEE Transactions on Audio, Speech, and Language Processing.
Cao, Shen, Sun, et al. 2007. “Detect and Track Latent Factors with Online Nonnegative Matrix Factorization.” In Proceedings of the 20th International Joint Conference on Artifical Intelligence. IJCAI’07.
Carabias-Orti, Virtanen, Vera-Candeas, et al. 2011. “Musical Instrument Sound Multi-Excitation Model for Non-Negative Spectrogram Factorization.” IEEE Journal of Selected Topics in Signal Processing.
Chen, and Chi. 2018. “Harnessing Structures in Big Data via Guaranteed Low-Rank Matrix Estimation: Recent Theory and Fast Algorithms via Convex and Nonconvex Optimization.” IEEE Signal Processing Magazine.
Chi, Lu, and Chen. 2019. “Nonconvex Optimization Meets Low-Rank Matrix Factorization: An Overview.” IEEE Transactions on Signal Processing.
Cichocki, Lee, Oseledets, et al. 2016. “Low-Rank Tensor Networks for Dimensionality Reduction and Large-Scale Optimization Problems: Perspectives and Challenges PART 1.” arXiv:1609.00893 [Cs].
Cichocki, Zdunek, and Amari. 2006. “New Algorithms for Non-Negative Matrix Factorization in Applications to Blind Source Separation.” In 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings.
Cohen, Daubechies, and Feauveau. 1992. “Biorthogonal Bases of Compactly Supported Wavelets.” Communications on Pure and Applied Mathematics.
Combettes, and Pesquet. 2008. “A Proximal Decomposition Method for Solving Convex Variational.” Inverse Problems.
Dasarathy, Shah, Bhaskar, et al. 2013. “Sketching Sparse Matrices.” arXiv:1303.6544 [Cs, Math].
Dasgupta, and Gupta. 2003. “An Elementary Proof of a Theorem of Johnson and Lindenstrauss.” Random Structures & Algorithms.
Davis. 1963. “The Rotation of Eigenvectors by a Perturbation.” Journal of Mathematical Analysis and Applications.
Defferrard, Bresson, and Vandergheynst. 2016. “Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering.” In Advances In Neural Information Processing Systems.
Del Moral, and Niclas. 2018. “A Taylor Expansion of the Square Root Matrix Functional.”
Desai, Ghashami, and Phillips. 2016. “Improved Practical Matrix Sketching with Guarantees.” IEEE Transactions on Knowledge and Data Engineering.
Devarajan. 2008. “Nonnegative Matrix Factorization: An Analytical and Interpretive Tool in Computational Biology.” PLoS Comput Biol.
Ding, He, and Simon. 2005. “On the Equivalence of Nonnegative Matrix Factorization and Spectral Clustering.” In Proceedings of the 2005 SIAM International Conference on Data Mining. Proceedings.
Ding, Li, and Jordan. 2010. “Convex and Semi-Nonnegative Matrix Factorizations.” IEEE Transactions on Pattern Analysis and Machine Intelligence.
Dokmanić, and Gribonval. 2017. “Beyond Moore-Penrose Part II: The Sparse Pseudoinverse.” arXiv:1706.08701 [Cs, Math].
Dolcetti, and Pertici. 2020. “Real Square Roots of Matrices: Differential Properties in Semi-Simple, Symmetric and Orthogonal Cases.”
Driedger, and Pratzlich. 2015. “Let It Bee – Towards NMF-Inspired Audio Mosaicing.” In Proceedings of ISMIR.
Drineas, Kannan, and Mahoney. 2006a. “Fast Monte Carlo Algorithms for Matrices II: Computing a Low-Rank Approximation to a Matrix.” SIAM Journal on Computing.
———. 2006b. “Fast Monte Carlo Algorithms for Matrices III: Computing a Compressed Approximate Matrix Decomposition.” SIAM Journal on Computing.
Drineas, and Mahoney. 2005. “On the Nyström Method for Approximating a Gram Matrix for Improved Kernel-Based Learning.” Journal of Machine Learning Research.
Dueck, Morris, and Frey. 2005. “Multi-Way Clustering of Microarray Data Using Probabilistic Sparse Matrix Factorization.” Bioinformatics.
Eaton. 2007a. “Chapter 5: Matrix Factorizations and Jacobians.” In Institute of Mathematical Statistics Lecture Notes - Monograph Series.
———. 2007b. Multivariate statistics: a vector space approach. Lecture notes-monograph series / Institute of Mathematical Statistics 53.
Ellis, and Lay. 1992. “Factorization of Finite Rank Hankel and Toeplitz Matrices.” Linear Algebra and Its Applications.
Fairbanks, Kannan, Park, et al. 2015. “Behavioral Clusters in Dynamic Graphs.” Parallel Computing, Graph analysis for scientific discovery,.
Fasi, Higham, and Liu. 2023. “Computing the Square Root of a Low-Rank Perturbation of the Scaled Identity Matrix.” SIAM Journal on Matrix Analysis and Applications.
Févotte, Bertin, and Durrieu. 2008. “Nonnegative Matrix Factorization with the Itakura-Saito Divergence: With Application to Music Analysis.” Neural Computation.
Flammia, Gross, Liu, et al. 2012. “Quantum Tomography via Compressed Sensing: Error Bounds, Sample Complexity, and Efficient Estimators.” New Journal of Physics.
Fung, Hariharan, Harvey, et al. 2011. “A General Framework for Graph Sparsification.” In Proceedings of the Forty-Third Annual ACM Symposium on Theory of Computing. STOC ’11.
Gemulla, Nijkamp, Haas, et al. 2011. “Large-Scale Matrix Factorization with Distributed Stochastic Gradient Descent.” In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’11.
Ghashami, Liberty, Phillips, et al. 2015. “Frequent Directions : Simple and Deterministic Matrix Sketching.” arXiv:1501.01711 [Cs].
Gordon. 2002. “Generalized² Linear² Models.” In Proceedings of the 15th International Conference on Neural Information Processing Systems. NIPS’02.
Gross, D. 2011. “Recovering Low-Rank Matrices From Few Coefficients in Any Basis.” IEEE Transactions on Information Theory.
Grosse, Salakhutdinov, Freeman, et al. 2012. “Exploiting Compositionality to Explore a Large Space of Model Structures.” In Proceedings of the Conference on Uncertainty in Artificial Intelligence.
Gross, David, Liu, Flammia, et al. 2010. “Quantum State Tomography via Compressed Sensing.” Physical Review Letters.
Guan, Naiyang, Tao, Luo, et al. 2012. “NeNMF: An Optimal Gradient Method for Nonnegative Matrix Factorization.” IEEE Transactions on Signal Processing.
Guan, N., Tao, Luo, et al. 2012. “Online Nonnegative Matrix Factorization With Robust Stochastic Approximation.” IEEE Transactions on Neural Networks and Learning Systems.
Gu, and Eisenstat. 1993. “A Stable and Fast Algorithm for Updating the Singular Value Decomposition.”
———. 1995. “Downdating the Singular Value Decomposition.” SIAM Journal on Matrix Analysis and Applications.
Hackbusch. 2015. Hierarchical Matrices: Algorithms and Analysis. Springer Series in Computational Mathematics 49.
Halko, Martinsson, Shkolnisky, et al. 2011. “An Algorithm for the Principal Component Analysis of Large Data Sets.” SIAM Journal on Scientific Computing.
Halko, Martinsson, and Tropp. 2010. “Finding Structure with Randomness: Probabilistic Algorithms for Constructing Approximate Matrix Decompositions.”
Harbrecht, Peters, and Schneider. 2012. “On the Low-Rank Approximation by the Pivoted Cholesky Decomposition.” Applied Numerical Mathematics, Third Chilean Workshop on Numerical Analysis of Partial Differential Equations (WONAPDE 2010),.
Harville. 1976. “Extension of the Gauss-Markov Theorem to Include the Estimation of Random Effects.” The Annals of Statistics.
———. 1977. “Maximum Likelihood Approaches to Variance Component Estimation and to Related Problems.” Journal of the American Statistical Association.
Hassanieh, Haitham, Indyk, Katabi, et al. 2012. “Nearly Optimal Sparse Fourier Transform.” In Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing. STOC ’12.
Hassanieh, H., Indyk, Katabi, et al. 2012. “Simple and Practical Algorithm for Sparse Fourier Transform.” In Proceedings of the Twenty-Third Annual ACM-SIAM Symposium on Discrete Algorithms. Proceedings.
Hastie, Mazumder, Lee, et al. 2015. “Matrix Completion and Low-Rank SVD via Fast Alternating Least Squares.” In Journal of Machine Learning Research.
Heinig, and Rost. 2011. “Fast Algorithms for Toeplitz and Hankel Matrices.” Linear Algebra and Its Applications.
Henderson, and Searle. 1981. “On Deriving the Inverse of a Sum of Matrices.” SIAM Review.
Hoffman, Matthew, Bach, and Blei. 2010. “Online Learning for Latent Dirichlet Allocation.” In Advances in Neural Information Processing Systems.
Hoffman, Matthew D, Blei, and Cook. 2010. “Bayesian Nonparametric Matrix Factorization for Recorded Music.” In International Conference on Machine Learning.
Hoyer. 2002. “Non-Negative Sparse Coding.” In Proceedings of the 2002 12th IEEE Workshop on Neural Networks for Signal Processing, 2002.
Hsieh, and Dhillon. 2011. “Fast Coordinate Descent Methods with Variable Selection for Non-Negative Matrix Factorization.” In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’11.
Huang, Kaess, and Leonard. 2013. “Consistent Sparsification for Graph Optimization.” In 2013 European Conference on Mobile Robots (ECMR).
Hu, Pehlevan, and Chklovskii. 2014. “A Hebbian/Anti-Hebbian Network for Online Sparse Dictionary Learning Derived from Symmetric Matrix Factorization.” In 2014 48th Asilomar Conference on Signals, Systems and Computers.
Huynh, Zhao, and Phung. 2020. “OTLDA: A Geometry-Aware Optimal Transport Approach for Topic Modeling.” In Advances in Neural Information Processing Systems.
Iliev, Stanev, Vesselinov, et al. 2018. “Nonnegative Matrix Factorization for Identification of Unknown Number of Sources Emitting Delayed Signals.” PLOS ONE.
Ji, Dunson, and Carin. 2009. “Multitask Compressive Sensing.” IEEE Transactions on Signal Processing.
Kannan. 2016. “Scalable and Distributed Constrained Low Rank Approximations.”
Kannan, Ballard, and Park. 2016. “A High-Performance Parallel Algorithm for Nonnegative Matrix Factorization.” In Proceedings of the 21st ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming. PPoPP ’16.
Keriven, Bourrier, Gribonval, et al. 2016. “Sketching for Large-Scale Learning of Mixture Models.” In 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).
Keshava. 2003. “A Survey of Spectral Unmixing Algorithms.” Lincoln Laboratory Journal.
Khoromskij, Litvinenko, and Matthies. 2009. “Application of Hierarchical Matrices for Computing the Karhunen–Loève Expansion.” Computing.
Kim, and Park. 2008. “Nonnegative Matrix Factorization Based on Alternating Nonnegativity Constrained Least Squares and Active Set Method.” SIAM Journal on Matrix Analysis and Applications.
Koren, Bell, and Volinsky. 2009. “Matrix Factorization Techniques for Recommender Systems.” Computer.
Koutis, Miller, and Peng. 2012. “A Fast Solver for a Class of Linear Systems.” Communications of the ACM.
Kruskal. 1964. “Nonmetric Multidimensional Scaling: A Numerical Method.” Psychometrika.
Kumar, and Shneider. 2016. “Literature Survey on Low Rank Approximation of Matrices.” arXiv:1606.06511 [Cs, Math].
Lahiri, Gao, and Ganguli. 2016. “Random Projections of Random Manifolds.” arXiv:1607.04331 [Cs, q-Bio, Stat].
Lawrence, and Urtasun. 2009. “Non-Linear Matrix Factorization with Gaussian Processes.” In Proceedings of the 26th Annual International Conference on Machine Learning. ICML ’09.
Lee, and Seung. 1999. “Learning the Parts of Objects by Non-Negative Matrix Factorization.” Nature.
———. 2001. “Algorithms for Non-Negative Matrix Factorization.” In Advances in Neural Information Processing Systems 13.
Liberty. 2013. “Simple and Deterministic Matrix Sketching.” In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’13.
Liberty, Woolfe, Martinsson, et al. 2007. “Randomized Algorithms for the Low-Rank Approximation of Matrices.” Proceedings of the National Academy of Sciences.
Li, S.Z., Hou, Zhang, et al. 2001. “Learning Spatially Localized, Parts-Based Representation.” In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2001. CVPR 2001.
Lim, and Teh. 2007. “Variational Bayesian Approach to Movie Rating Prediction.” In Proceedings of KDD Cup and Workshop.
Lin, Chih-Jen. 2007. “Projected Gradient Methods for Nonnegative Matrix Factorization.” Neural Computation.
Lin, Zhouchen. 2016. “A Review on Low-Rank Models in Signal and Data Analysis.”
Li, Chi-Kwong, and Poon. 2002. “Additive Decomposition of Real Matrices.” Linear and Multilinear Algebra.
Liu, T., and Tao. 2015. “On the Performance of Manhattan Nonnegative Matrix Factorization.” IEEE Transactions on Neural Networks and Learning Systems.
Liu, Tongliang, Tao, and Xu. 2016. “Dimensionality-Dependent Generalization Bounds for \(k\)-Dimensional Coding Schemes.” arXiv:1601.00238 [Cs, Stat].
López-Serrano, Dittmar, Özer, et al. 2019. “NMF Toolbox: Music Processing Applications of Nonnegative Matrix Factorization.” In.
Mahoney. 2010. Randomized Algorithms for Matrices and Data.
Mailhé, Gribonval, Vandergheynst, et al. 2011. “Fast Orthogonal Sparse Approximation Algorithms over Local Dictionaries.” Signal Processing, Advances in Multirate Filter Bank Structures and Multiscale Representations,.
Mairal, Bach, Ponce, et al. 2009. “Online Dictionary Learning for Sparse Coding.” In Proceedings of the 26th Annual International Conference on Machine Learning. ICML ’09.
———, et al. 2010. “Online Learning for Matrix Factorization and Sparse Coding.” The Journal of Machine Learning Research.
Mairal, Bach, and Ponce. 2014. Sparse Modeling for Image and Vision Processing.
Martinsson. 2016. “Randomized Methods for Matrix Computations and Analysis of High Dimensional Data.” arXiv:1607.01649 [Math].
Martinsson, Rockhlin, and Tygert. 2006. “A Randomized Algorithm for the Approximation of Matrices.”
Mensch, Mairal, Thirion, et al. 2017. “Stochastic Subsampling for Factorizing Huge Matrices.” arXiv:1701.05363 [Math, q-Bio, Stat].
Minka. 2000. Old and new matrix algebra useful for statistics.
Mnih, and Salakhutdinov. 2008. “Probabilistic Matrix Factorization.” Advances in Neural Information Processing Systems.
Mohamed. 2011. “Generalised Bayesian Matrix Factorisation Models.”
Nakajima, and Sugiyama. 2012. “Theoretical Analysis of Bayesian Matrix Factorization.” Journal of Machine Learning Research.
Nakatsukasa. 2019. “The Low-Rank Eigenvalue Problem.”
Needell, and Vershynin. 2009. “Uniform Uncertainty Principle and Signal Recovery via Regularized Orthogonal Matching Pursuit.” Foundations of Computational Mathematics.
Nowak, and Litvinenko. 2013. “Kriging and Spatial Design Accelerated by Orders of Magnitude: Combining Low-Rank Covariance Approximations with FFT-Techniques.” Mathematical Geosciences.
Okajima, and Kabashima. 2021. “Matrix Completion Based on Gaussian Parameterized Belief Propagation.”
Oymak, and Tropp. 2015. “Universality Laws for Randomized Dimension Reduction, with Applications.” arXiv:1511.09433 [Cs, Math, Stat].
Paatero, and Tapper. 1994. “Positive Matrix Factorization: A Non-Negative Factor Model with Optimal Utilization of Error Estimates of Data Values.” Environmetrics.
Pan, Zhang, Wu, et al. 2014. “Online Community Detection for Large Complex Networks.” PLoS ONE.
Petersen, and Pedersen. 2012. “The Matrix Cookbook.”
Pleiss, Gardner, Weinberger, et al. 2018. “Constant-Time Predictive Distributions for Gaussian Processes.” In.
Pleiss, Jankowiak, Eriksson, et al. 2020. “Fast Matrix Square Roots with Applications to Gaussian Processes and Bayesian Optimization.” Advances in Neural Information Processing Systems.
Rabani, and Toledo. 2001. “Out-of-Core SVD and QR Decompositions.” In PPSC.
Raiko, Ilin, and Karhunen. 2007. “Principal Component Analysis for Large Scale Problems with Lots of Missing Values.” In Machine Learning: ECML 2007.
Rokhlin, Szlam, and Tygert. 2009. “A Randomized Algorithm for Principal Component Analysis.” SIAM J. Matrix Anal. Appl.
Rokhlin, and Tygert. 2008. “A Fast Randomized Algorithm for Overdetermined Linear Least-Squares Regression.” Proceedings of the National Academy of Sciences.
Ryabko, and Ryabko. 2010. “Nonparametric Statistical Inference for Ergodic Processes.” IEEE Transactions on Information Theory.
Saad. 2003. Iterative Methods for Sparse Linear Systems: Second Edition.
Sachdeva, Sushant. 2013. “Faster Algorithms via Approximation Theory.” Foundations and Trends® in Theoretical Computer Science.
Sachdeva, Noveen, Dhaliwal, Wu, et al. 2022. “Infinite Recommendation Networks: A Data-Centric Approach.”
Salakhutdinov, and Mnih. 2008. “Bayesian Probabilistic Matrix Factorization Using Markov Chain Monte Carlo.” In Proceedings of the 25th International Conference on Machine Learning. ICML ’08.
Sarwar, Karypis, Konstan, et al. 2002. “Incremental Singular Value Decomposition Algorithms for Highly Scalable Recommender Systems.”
Saul. 2023. “A Geometrical Connection Between Sparse and Low-Rank Matrices and Its Application to Manifold Learning.” Transactions on Machine Learning Research.
Schmidt, Larsen, and Hsiao. 2007. “Wind Noise Reduction Using Non-Negative Sparse Coding.” In 2007 IEEE Workshop on Machine Learning for Signal Processing.
Seeger, ed. 2004. Low Rank Updates for the Cholesky Decomposition.
Seshadhri, Sharma, Stolman, et al. 2020. “The Impossibility of Low-Rank Representations for Triangle-Rich Complex Networks.” Proceedings of the National Academy of Sciences.
Shi, Zheng, and Yang. 2017. “Survey on Probabilistic Models of Low-Rank Matrix Factorizations.” Entropy.
Singh, and Gordon. 2008. “A Unified View of Matrix Factorization Models.” In Machine Learning and Knowledge Discovery in Databases.
Smaragdis. 2004. “Non-Negative Matrix Factor Deconvolution; Extraction of Multiple Sound Sources from Monophonic Inputs.” In Independent Component Analysis and Blind Signal Separation. Lecture Notes in Computer Science.
Soh, and Chandrasekaran. 2017. “A Matrix Factorization Approach for Learning Semidefinite-Representable Regularizers.” arXiv:1701.01207 [Cs, Math, Stat].
Song, Sebe, and Wang. 2022. “Fast Differentiable Matrix Square Root.” In.
Sorzano, Vargas, and Montano. 2014. “A Survey of Dimensionality Reduction Techniques.” arXiv:1403.2877 [Cs, q-Bio, Stat].
Spielman, D., and Srivastava. 2011. “Graph Sparsification by Effective Resistances.” SIAM Journal on Computing.
Spielman, Daniel A., and Teng. 2004. “Nearly-Linear Time Algorithms for Graph Partitioning, Graph Sparsification, and Solving Linear Systems.” In Proceedings of the Thirty-Sixth Annual ACM Symposium on Theory of Computing. STOC ’04.
———. 2006. “Nearly-Linear Time Algorithms for Preconditioning and Solving Symmetric, Diagonally Dominant Linear Systems.” arXiv:cs/0607105.
———. 2008a. “Spectral Sparsification of Graphs.” arXiv:0808.4134 [Cs].
———. 2008b. “A Local Clustering Algorithm for Massive Graphs and Its Application to Nearly-Linear Time Graph Partitioning.” arXiv:0809.3232 [Cs].
Sra, and Dhillon. 2006. “Generalized Nonnegative Matrix Approximations with Bregman Divergences.” In Advances in Neural Information Processing Systems 18.
Srebro, Rennie, and Jaakkola. 2004. “Maximum-Margin Matrix Factorization.” In Advances in Neural Information Processing Systems. NIPS’04.
Stewart. 2000. “The Decompositional Approach to Matrix Computation.” Computing in Science Engineering.
Sundin. 2016. “Bayesian Methods for Sparse and Low-Rank Matrix Problems.”
Sun, and Stein. 2016. “Statistically and Computationally Efficient Estimating Equations for Large Spatial Datasets.” Journal of Computational and Graphical Statistics.
Tropp, Yurtsever, Udell, et al. 2016. “Randomized Single-View Algorithms for Low-Rank Matrix Approximation.” arXiv:1609.00048 [Cs, Math, Stat].
———, et al. 2017. “Practical Sketching Algorithms for Low-Rank Matrix Approximation.” SIAM Journal on Matrix Analysis and Applications.
Tufts, and Kumaresan. 1982. “Estimation of Frequencies of Multiple Sinusoids: Making Linear Prediction Perform Like Maximum Likelihood.” Proceedings of the IEEE.
Tung, and Little. n.d. “Factorized Binary Codes for Large-Scale Nearest Neighbor Search.”
Türkmen. 2015. “A Review of Nonnegative Matrix Factorization Methods for Clustering.” arXiv:1507.03194 [Cs, Stat].
Turner, and Sahani. 2014. “Time-Frequency Analysis as Probabilistic Inference.” IEEE Transactions on Signal Processing.
Udell, and Townsend. 2019. “Why Are Big Data Matrices Approximately Low Rank?” SIAM Journal on Mathematics of Data Science.
Vaz, Toutios, and Narayanan. 2016. “Convex Hull Convolutive Non-Negative Matrix Factorization for Uncovering Temporal Patterns in Multivariate Time-Series Data.” In.
Vincent, Bertin, and Badeau. 2008. “Harmonic and Inharmonic Nonnegative Matrix Factorization for Polyphonic Pitch Transcription.” In 2008 IEEE International Conference on Acoustics, Speech and Signal Processing.
Virtanen. 2007. “Monaural Sound Source Separation by Nonnegative Matrix Factorization With Temporal Continuity and Sparseness Criteria.” IEEE Transactions on Audio, Speech, and Language Processing.
Vishnoi. 2013. “Lx = b.” Foundations and Trends® in Theoretical Computer Science.
Vo, Vo, and Hoang. 2017. “An Efficient Implementation of the Generalized Labeled Multi-Bernoulli Filter.” arXiv:1606.08350 [Stat].
Wager, Chen, Kim, et al. 2017. “Towards Expressive Instrument Synthesis Through Smooth Frame-by-Frame Reconstruction: From String to Woodwind.” In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).
Wang, Shusen, Gittens, and Mahoney. 2017. “Sketched Ridge Regression: Optimization Perspective, Statistical Perspective, and Model Averaging.” arXiv:1702.04837 [Cs, Stat].
Wang, Boyue, Hu, Gao, et al. 2017. “Locality Preserving Projections for Grassmann Manifold.” In PRoceedings of IJCAI, 2017.
Wang, Yuan, and Jia. 2004. “Fisher Non-Negative Matrix Factorization for Learning Local Features.” In In Proc. Asian Conf. On Comp. Vision.
Wang, Sinong, Li, Khabsa, et al. 2020. “Linformer: Self-Attention with Linear Complexity.”
Wang, Y. X., and Zhang. 2013. “Nonnegative Matrix Factorization: A Comprehensive Review.” IEEE Transactions on Knowledge and Data Engineering.
Wilkinson, Andersen, Reiss, et al. 2019. “End-to-End Probabilistic Inference for Nonstationary Audio Analysis.” arXiv:1901.11436 [Cs, Eess, Stat].
Woodruff. 2014. Sketching as a Tool for Numerical Linear Algebra. Foundations and Trends in Theoretical Computer Science 1.0.
Woolfe, Liberty, Rokhlin, et al. 2008. “A Fast Randomized Algorithm for the Approximation of Matrices.” Applied and Computational Harmonic Analysis.
Wright, and Ma. 2022. High-dimensional data analysis with low-dimensional models: Principles, computation, and applications.
Xinghao Ding, Lihan He, and Carin. 2011. “Bayesian Robust Principal Component Analysis.” IEEE Transactions on Image Processing.
Yang, Linxiao, Fang, Duan, et al. 2018. “Fast Low-Rank Bayesian Matrix Completion with Hierarchical Gaussian Prior Models.” IEEE Transactions on Signal Processing.
Yang, Jiyan, Meng, and Mahoney. 2015. “Implementing Randomized Matrix Algorithms in Parallel and Distributed Environments.” arXiv:1502.03032 [Cs, Math, Stat].
Yang, Wenzhuo, and Xu. 2015. “Streaming Sparse Principal Component Analysis.” In Journal of Machine Learning Research.
Ye, and Lim. 2016. “Every Matrix Is a Product of Toeplitz Matrices.” Foundations of Computational Mathematics.
Yin, Gao, and Lin. 2016. “Laplacian Regularized Low-Rank Representation and Its Applications.” IEEE Transactions on Pattern Analysis and Machine Intelligence.
Yoshii. 2013. “Beyond NMF: Time-Domain Audio Source Separation Without Phase Reconstruction.”
Yu, Hsiang-Fu, Hsieh, Si, et al. 2012. “Scalable Coordinate Descent Approaches to Parallel Matrix Factorization for Recommender Systems.” In IEEE International Conference of Data Mining.
———, et al. 2014. “Parallel Matrix Factorization for Recommender Systems.” Knowledge and Information Systems.
Yu, Chenhan D., March, and Biros. 2017. “An \(N \log N\) Parallel Fast Direct Solver for Kernel Matrices.” In arXiv:1701.02324 [Cs].
Yurtsever, Tropp, Fercoq, et al. 2021. “Scalable Semidefinite Programming.” SIAM Journal on Mathematics of Data Science.
Zass, and Shashua. 2005. “A Unifying Approach to Hard and Probabilistic Clustering.” In Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV’05) Volume 1 - Volume 01. ICCV ’05.
Zhang, Yangwen. 2022. “An Answer to an Open Question in the Incremental SVD.”
Zhang, Zhongyuan, Ding, Li, et al. 2007. “Binary Matrix Factorization with Applications.” In Seventh IEEE International Conference on Data Mining, 2007. ICDM 2007.
Zhang, Kai, Liu, Zhang, et al. 2017. “Randomization or Condensation?: Linear-Cost Matrix Sketching Via Cascaded Compression Sampling.” In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. KDD ’17.
Zhang, Xiao, Wang, and Gu. 2017. “Stochastic Variance-Reduced Gradient Descent for Low-Rank Matrix Recovery from Linear Measurements.” arXiv:1701.00481 [Stat].
Zhao, Du, Buntine, et al. 2018. “Inter and Intra Topic Structure Learning with Word Embeddings.” In Proceedings of the 35th International Conference on Machine Learning.
Zhao, Phung, Huynh, et al. 2020. “Neural Topic Model via Optimal Transport.” In.
Zhou, Mingyuan, Chen, Paisley, et al. 2009. “Non-Parametric Bayesian Dictionary Learning for Sparse Image Representations.” In Proceedings of the 22nd International Conference on Neural Information Processing Systems. NIPS’09.
Zhou, Mingyuan, Hannah, Dunson, et al. 2012. “Beta-Negative Binomial Process and Poisson Factor Analysis.” In Proceedings of the Fifteenth International Conference on Artificial Intelligence and Statistics.
Zhou, Tianyi, and Tao. 2011. “GoDec: Randomized Low-Rank & Sparse Matrix Decomposition in Noisy Case.” In Proceedings of the 28th International Conference on International Conference on Machine Learning. ICML’11.
———. 2012. “Multi-Label Subspace Ensemble.” Journal of Machine Learning Research.
Zitnik, and Zupan. 2018. “NIMFA: A Python Library for Nonnegative Matrix Factorization.” arXiv:1808.01743 [Cs, q-Bio, Stat].