Markov Chain Monte Carlo methods

August 28, 2017 — June 8, 2022

Bayes
estimator distribution
generative
Markov processes
Monte Carlo
probabilistic algorithms
probability
Figure 1: This chain pump is not a good metaphor for how a Markov chain Monte Carlo sampler works, but it does correctly evoke the effort involved.

Despite studying within this area, I have nothing to say about MCMC broadly, but I do have some things I wish to keep notes on.

1 Hamiltonian Monte Carlo

A method inspired by conservation laws in physics.

2 Connection to variational inference

Deep. See (Salimans, Kingma, and Welling 2015)

3 Adaptive MCMC

See Adaptive MCMC.

4 Stochastic Gradient Monte carlo

See SGD MCMC.

5 Tempering

e.g. Ge, Lee, and Risteski (2020);Syed et al. (2020). Saif Syed can explain this quite well. Or, as Lee and Risteski put it:

The main idea is to create a meta-Markov chain (the simulated tempering chain) which has two types of moves: change the current “temperature” of the sample, or move “within” a temperature. The main intuition behind this is that at higher temperatures, the distribution is flatter, so the chain explores the landscape faster.

Figure 2

6 Mixing rates

See ergodic theorems and mixing.

7 Debiasing via coupling

Pierre E. Jacob, John O’Leary, Yves Atchadé, crediting Glynn and Rhee (2014), made MCMC estimators without finite-time-bias, which is nice for parallelisation (Jacob, O’Leary, and Atchadé 2019).

8 Affine invariant

J. Goodman and Weare (2010)

We propose a family of Markov chain Monte Carlo methods whose performance is unaffected by affine transformations of space. These algorithms are easy to construct and require little or no additional computational overhead. They should be particularly useful for sampling badly scaled distributions. Computational tests show that the affine invariant methods can be significantly faster than standard MCMC methods on highly skewed distributions.

Implemented in, e.g. emcee (Foreman-Mackey et al. 2013).

9 Efficiency of

Want to adaptively tune the MCMC? See tuning MCMC.

10 Incoming

11 References

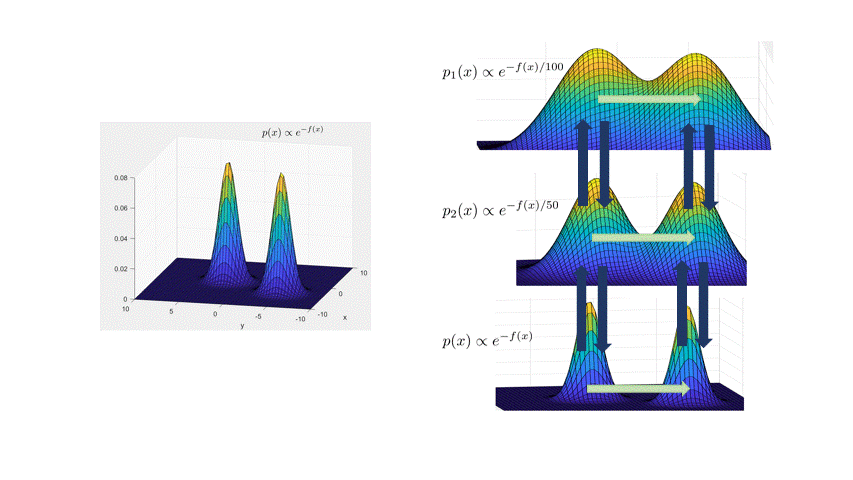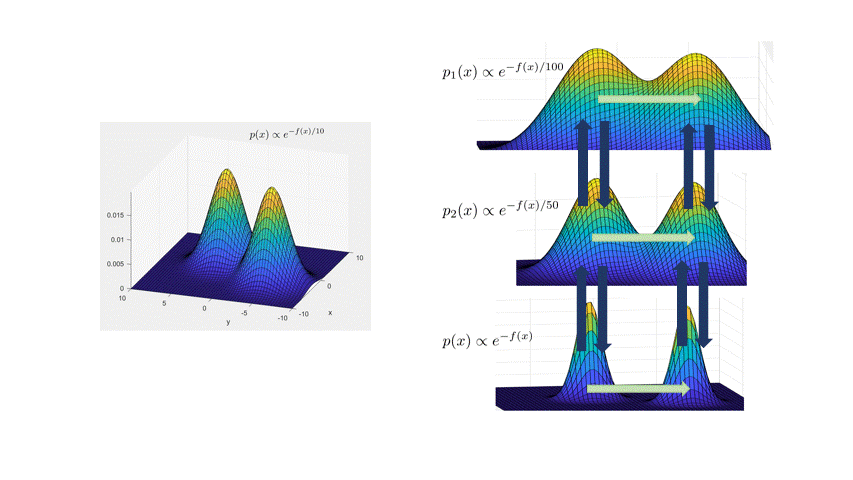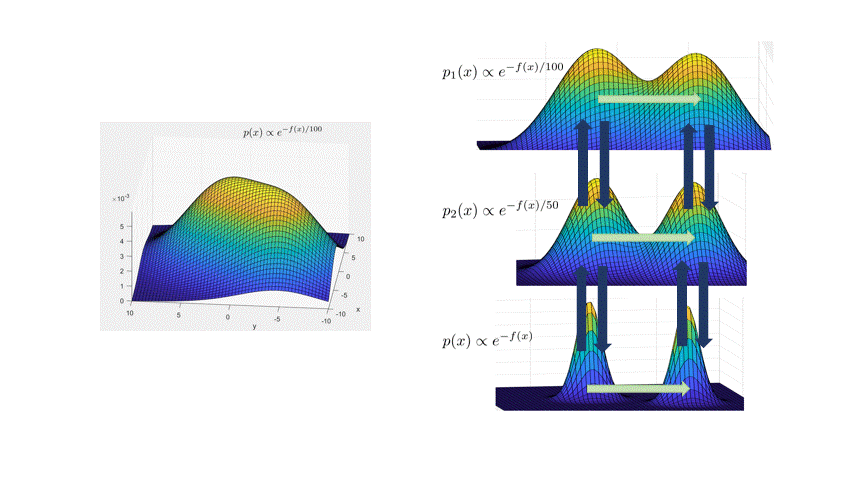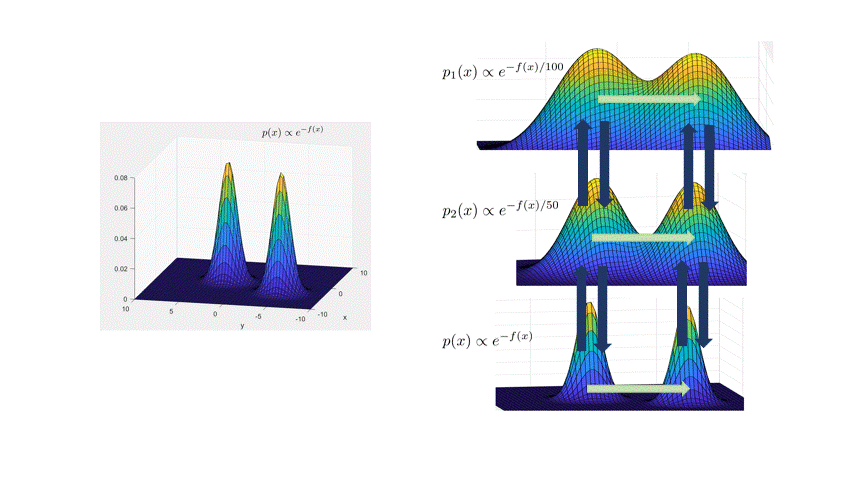
Andrieu, and Thoms. 2008. “A Tutorial on Adaptive MCMC.” Statistics and Computing.
Atchadé, Fort, Moulines, et al. 2011. “Adaptive Markov Chain Monte Carlo: Theory and Methods.” In Bayesian Time Series Models.
Au, Graham, and Thiery. 2020. “Manifold Lifting: Scaling MCMC to the Vanishing Noise Regime.”
Bach. 2015. “On the Equivalence Between Kernel Quadrature Rules and Random Feature Expansions.”
Bales, Pourzanjani, Vehtari, et al. 2019. “Selecting the Metric in Hamiltonian Monte Carlo.” arXiv:1905.11916 [Stat].
Betancourt. 2017. “A Conceptual Introduction to Hamiltonian Monte Carlo.” arXiv:1701.02434 [Stat].
———. 2018. “The Convergence of Markov Chain Monte Carlo Methods: From the Metropolis Method to Hamiltonian Monte Carlo.” Annalen Der Physik.
———. 2021. “A Short Review of Ergodicity and Convergence of Markov Chain Monte Carlo Estimators.” arXiv:2110.07032 [Math, Stat].
Betancourt, Byrne, Livingstone, et al. 2017. “The Geometric Foundations of Hamiltonian Monte Carlo.” Bernoulli.
Bousquet, Luxburg, and Rtsch. 2004. Advanced Lectures on Machine Learning: ML Summer Schools 2003, Canberra, Australia, February 2-14, 2003, T Bingen, Germany, August 4-16, 2003, Revised Lectures.
Brosse, Moulines, and Durmus. 2018. “The Promises and Pitfalls of Stochastic Gradient Langevin Dynamics.” In Proceedings of the 32nd International Conference on Neural Information Processing Systems. NIPS’18.
Calderhead. 2014. “A General Construction for Parallelizing Metropolis−Hastings Algorithms.” Proceedings of the National Academy of Sciences.
Carpenter, Hoffman, Brubaker, et al. 2015. “The Stan Math Library: Reverse-Mode Automatic Differentiation in C++.” arXiv Preprint arXiv:1509.07164.
Caterini, Doucet, and Sejdinovic. 2018. “Hamiltonian Variational Auto-Encoder.” In Advances in Neural Information Processing Systems.
Chakraborty, Bhattacharya, and Khare. 2019. “Estimating Accuracy of the MCMC Variance Estimator: A Central Limit Theorem for Batch Means Estimators.” arXiv:1911.00915 [Math, Stat].
Cornish, Vanetti, Bouchard-Côté, et al. 2019. “Scalable Metropolis-Hastings for Exact Bayesian Inference with Large Datasets.” arXiv:1901.09881 [Cs, Stat].
Cotter, Roberts, Stuart, et al. 2013. “MCMC Methods for Functions: Modifying Old Algorithms to Make Them Faster.” Statistical Science.
Dhaka, and Catalina. 2020. “Robust, Accurate Stochastic Optimization for Variational Inference.”
Diaconis, and Freedman. 1999. “Iterated Random Functions.” SIAM Review.
Durmus, and Moulines. 2016. “High-Dimensional Bayesian Inference via the Unadjusted Langevin Algorithm.” arXiv:1605.01559 [Math, Stat].
Fan, and Sisson. 2010. “Reversible Jump Markov Chain Monte Carlo.”
Foreman-Mackey, Hogg, Lang, et al. 2013. “Emcee: The MCMC Hammer.” Publications of the Astronomical Society of the Pacific.
Ge, Lee, and Risteski. 2020. “Simulated Tempering Langevin Monte Carlo II: An Improved Proof Using Soft Markov Chain Decomposition.” arXiv:1812.00793 [Cs, Math, Stat].
Girolami, and Calderhead. 2011. “Riemann Manifold Langevin and Hamiltonian Monte Carlo Methods.” Journal of the Royal Statistical Society: Series B (Statistical Methodology).
Glynn, and Rhee. 2014. “Exact Estimation for Markov Chain Equilibrium Expectations.” Journal of Applied Probability.
Goodman, Noah, Mansinghka, Roy, et al. 2012. “Church: A Language for Generative Models.” arXiv:1206.3255.
Goodman, Jonathan, and Weare. 2010. “Ensemble Samplers with Affine Invariance.” Communications in Applied Mathematics and Computational Science.
Goodrich, Gelman, Hoffman, et al. 2017. “Stan : A Probabilistic Programming Language.” Journal of Statistical Software.
Hodgkinson, Salomone, and Roosta. 2019. “Implicit Langevin Algorithms for Sampling From Log-Concave Densities.” arXiv:1903.12322 [Cs, Stat].
Huang, and Gelman. 2005. “Sampling for Bayesian Computation with Large Datasets.” SSRN Electronic Journal.
Jacob, O’Leary, and Atchadé. 2019. “Unbiased Markov Chain Monte Carlo with Couplings.” arXiv:1708.03625 [Stat].
Jolicoeur-Martineau, Li, Piché-Taillefer, et al. 2021. “Gotta Go Fast When Generating Data with Score-Based Models.”
Korattikara, Chen, and Welling. 2015. “Sequential Tests for Large-Scale Learning.” Neural Computation.
Lele, S. R., Dennis, and Lutscher. 2007. “Data Cloning: Easy Maximum Likelihood Estimation for Complex Ecological Models Using Bayesian Markov Chain Monte Carlo Methods.” Ecology Letters.
Lele, Subhash R., Nadeem, and Schmuland. 2010. “Estimability and Likelihood Inference for Generalized Linear Mixed Models Using Data Cloning.” Journal of the American Statistical Association.
Liu. 1996. “Metropolized Independent Sampling with Comparisons to Rejection Sampling and Importance Sampling.” Statistics and Computing.
Ma, Chen, and Fox. 2015. “A Complete Recipe for Stochastic Gradient MCMC.” In Proceedings of the 28th International Conference on Neural Information Processing Systems - Volume 2. NIPS’15.
Mangoubi, and Smith. 2017. “Rapid Mixing of Hamiltonian Monte Carlo on Strongly Log-Concave Distributions.” arXiv:1708.07114 [Math, Stat].
Margossian, Vehtari, Simpson, et al. 2020. “Hamiltonian Monte Carlo Using an Adjoint-Differentiated Laplace Approximation: Bayesian Inference for Latent Gaussian Models and Beyond.” arXiv:2004.12550 [Stat].
Marzouk, Moselhy, Parno, et al. 2016. “Sampling via Measure Transport: An Introduction.” In Handbook of Uncertainty Quantification.
Neal. 1993. “Probabilistic Inference Using Markov Chain Monte Carlo Methods.” Technical Report CRGTR-93-1.
———. 2004. “Improving Asymptotic Variance of MCMC Estimators: Non-Reversible Chains Are Better.” arXiv:math/0407281.
———. 2011. “MCMC Using Hamiltonian Dynamics.” In Handbook for Markov Chain Monte Carlo.
Nitanda, Wu, and Suzuki. 2020. “Particle Dual Averaging: Optimization of Mean Field Neural Networks with Global Convergence Rate Analysis.” arXiv:2012.15477 [Cs, Stat].
Norton, and Fox. 2016. “Tuning of MCMC with Langevin, Hamiltonian, and Other Stochastic Autoregressive Proposals.” arXiv:1610.00781 [Math, Stat].
Parno, and Marzouk. 2018. “Transport Map Accelerated Markov Chain Monte Carlo.” SIAM/ASA Journal on Uncertainty Quantification.
Plummer. 2023. “Simulation-Based Bayesian Analysis.” Annual Review of Statistics and Its Application.
Propp, and Wilson. 1996. “Exact Sampling with Coupled Markov Chains and Applications to Statistical Mechanics.” In Random Structures & Algorithms.
———. 1998. “Coupling from the Past: A User’s Guide.” In Microsurveys in Discrete Probability. DIMACS Series in Discrete Mathematics and Theoretical Computer Science.
Robert, Elvira, Tawn, et al. 2018. “Accelerating MCMC Algorithms.” WIREs Computational Statistics.
Roberts, Gareth O., and Rosenthal. 2004. “General State Space Markov Chains and MCMC Algorithms.” Probability Surveys.
Roberts, G.O., and Smith. 1994. “Simple Conditions for the Convergence of the Gibbs Sampler and Metropolis-Hastings Algorithms.” Stochastic Processes and Their Applications.
Rubinstein, Reuven Y, and Kroese. 2004. The Cross-Entropy Method a Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation and Machine Learning.
Rubinstein, Reuven Y., and Kroese. 2016. Simulation and the Monte Carlo Method. Wiley series in probability and statistics.
Rubinstein, Reuven Y., Ridder, and Vaisman. 2014. Fast Sequential Monte Carlo Methods for Counting and Optimization. Wiley Series in Probability and Statistics.
Salimans, Kingma, and Welling. 2015. “Markov Chain Monte Carlo and Variational Inference: Bridging the Gap.” In Proceedings of the 32nd International Conference on Machine Learning (ICML-15). ICML’15.
Schuster, Strathmann, Paige, et al. 2017. “Kernel Sequential Monte Carlo.” In ECML-PKDD 2017.
Sisson, Fan, and Tanaka. 2007. “Sequential Monte Carlo Without Likelihoods.” Proceedings of the National Academy of Sciences.
Syed, Bouchard-Côté, Deligiannidis, et al. 2020. “Non-Reversible Parallel Tempering: A Scalable Highly Parallel MCMC Scheme.” arXiv:1905.02939 [Stat].
Vehtari, Gelman, Sivula, et al. 2019. “Expectation Propagation as a Way of Life: A Framework for Bayesian Inference on Partitioned Data.” arXiv:1412.4869 [Stat].
Wang, and Dunson. 2013. “Parallelizing MCMC via Weierstrass Sampler.”
Welling, and Teh. 2011. “Bayesian Learning via Stochastic Gradient Langevin Dynamics.” In Proceedings of the 28th International Conference on International Conference on Machine Learning. ICML’11.
Xifara, Sherlock, Livingstone, et al. 2014. “Langevin Diffusions and the Metropolis-Adjusted Langevin Algorithm.” Statistics & Probability Letters.
Xu, Zuheng, Chen, and Campbell. 2023. “MixFlows: Principled Variational Inference via Mixed Flows.”
Xu, Kai, Ge, Tebbutt, et al. 2019. “AdvancedHMC.jl: A Robust, Modular and Efficient Implementation of Advanced HMC Algorithms.”
Yoshida, and West. 2010. “Bayesian Learning in Sparse Graphical Factor Models via Variational Mean-Field Annealing.” Journal of Machine Learning Research.